Дерево двоичного поиска: различия между версиями
KVN (обсуждение | вклад) |
KVN (обсуждение | вклад) Нет описания правки |
||
| Строка 7: | Строка 7: | ||
в) для всякого числа <math>a \in S</math> существует единственная вершина <math>v</math>, для которой <math>l(v)=a</math>. | в) для всякого числа <math>a \in S</math> существует единственная вершина <math>v</math>, для которой <math>l(v)=a</math>. | ||
Другое название — ''Поисковое дерево''. | Другое название — ''[[Поисковое дерево]]'', ''[[Бинарное дерево поиска]]'', ''[[Дерево поиска]]''. | ||
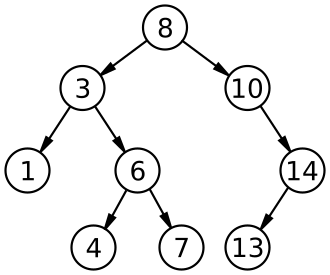
[[Файл: Binary_search_tree.png|275px]] | [[Файл: Binary_search_tree.png|275px]] | ||
Текущая версия от 09:11, 23 ноября 2024
Деревом двоичного поиска (Binary search tree) для множества чисел [math]\displaystyle{ S }[/math] называется помеченное бинарное дерево, в котором каждая вершина [math]\displaystyle{ v }[/math] помечена числом [math]\displaystyle{ l(v)\in S }[/math] и которое удовлетворяет следующим условиям:
а) [math]\displaystyle{ l(u)\lt l(v) }[/math] для всех вершин [math]\displaystyle{ u,v }[/math], если вершина [math]\displaystyle{ u }[/math] находится в левом поддереве вершины [math]\displaystyle{ v }[/math] (т.е. в поддереве, корень которого --- левый сын [math]\displaystyle{ v }[/math]);
б) [math]\displaystyle{ l(u)\gt l(v) }[/math] для всех вершин [math]\displaystyle{ u,v }[/math], если вершина [math]\displaystyle{ u }[/math] находится в правом поддереве вершины [math]\displaystyle{ v }[/math] (т.е. в поддереве, корень которого --- правый сын [math]\displaystyle{ v }[/math]);
в) для всякого числа [math]\displaystyle{ a \in S }[/math] существует единственная вершина [math]\displaystyle{ v }[/math], для которой [math]\displaystyle{ l(v)=a }[/math].
Другое название — Поисковое дерево, Бинарное дерево поиска, Дерево поиска.
Литература
- Касьянов В.Н., Поттосин И.В. Методы построения трансляторов. — Новосибирск: Наука. Сиб. отд-ние, 1986.
- Касьянов В. Н., Сабельфельд В. К. Сборник заданий по практикуму на ЭВМ. - М.: Наука, 1986.