Ротационный код: различия между версиями
KEV (обсуждение | вклад) Нет описания правки |
KVN (обсуждение | вклад) Нет описания правки |
||
| Строка 24: | Строка 24: | ||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | * Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | ||
[[Категория: Коды деревьев]] | |||
Версия от 08:23, 9 октября 2019
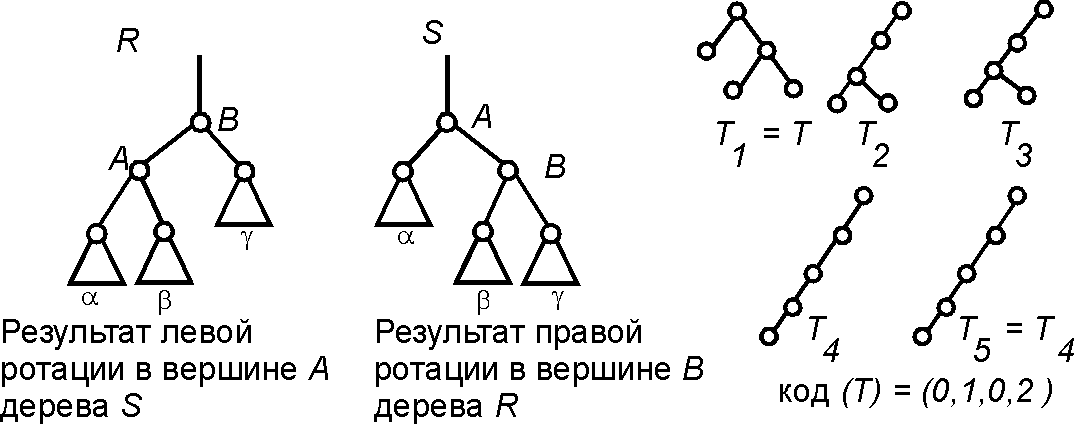
Ротационный код (Scheme using rotations) — Рассматриваются два вида преобразований бинарных деревьев в бинарные деревья: правая и левая ротация. Если бинарное дерево [math]\displaystyle{ \,D_1 }[/math] содержит поддерево [math]\displaystyle{ \,T_1=((\alpha ,A,\beta ),B,\gamma ) }[/math], где [math]\displaystyle{ \,A,\, B }[/math] — вершины, а [math]\displaystyle{ \,\alpha,\,\beta,\,\gamma }[/math] — произвольные поддеревья, то дерево [math]\displaystyle{ \,D_2 }[/math], в котором [math]\displaystyle{ \,T_1 }[/math] заменено на поддерево [math]\displaystyle{ \,T_2=(\alpha ,A,(\beta ,B,\gamma )) }[/math], является результатом правой ротации [math]\displaystyle{ \,D_1 }[/math] в вершине [math]\displaystyle{ \,B }[/math], а дерево [math]\displaystyle{ \,D_1 }[/math] является результатом левой ротации дерева [math]\displaystyle{ \,D_2 }[/math] в вершине [math]\displaystyle{ \,A }[/math]. Левая (правая) ротация в вершине [math]\displaystyle{ \,A }[/math] дерева [math]\displaystyle{ \,D }[/math] имеет глубину [math]\displaystyle{ \,k }[/math], если [math]\displaystyle{ \,k }[/math] — порядковый номер вершины [math]\displaystyle{ \,A }[/math] на пути по дереву [math]\displaystyle{ \,D }[/math] от его корня к самому левому листу.
Последовательность [math]\displaystyle{ (x_{n-1},x_{n-2}, \ldots ,x_2,x_1) }[/math] называется ротационным кодом дерева [math]\displaystyle{ \,D }[/math], если есть последовательность деревьев [math]\displaystyle{ D_n,D_{n-1},\ldots ,D_1 }[/math], в которой [math]\displaystyle{ \,D_1=D,\,D_n }[/math] — левостороннее дерево, а каждое дерево [math]\displaystyle{ \,D_{i+1} }[/math] получается из [math]\displaystyle{ \,D_i }[/math] применением [math]\displaystyle{ x_i }[/math] левых ротаций глубины [math]\displaystyle{ \,i }[/math].
См. также
- Коды Закса,
- Коды Ли,
- Коды, свободные от повторений,
- Коды с дублированием номеров вершин,
- Коды с использованием ограничителей,
- Линейный код,
- Уровневые коды корневых деревьев.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.